Introduction
Le diagramme de corrélation ou diagramme de dispersion (ou scatter diagram en anglais) est un outil de contrôle et d’aide à la décision pour vérifier l’existence d’une relation cause-effet entre deux variables de nature quantitative.
Cet diagramme s’utilise dans un contexte de production où l’on veut connaître la racine d’un problème et améliorer la performance ou comprendre certains phénomènes. Il peut aussi être utilisé dans un contexte d’amélioration de la qualité où l’on veut mesurer l’impact des efforts d’amélioration sur les résultats de production.
Table of Contents
A quoi sert le diagramme de corrélation ?
Le diagramme de corrélation ou de dispersion est un outil utilisé dans plusieurs domaines, y inclus le domaine de la qualité, pour explorer la relation entre deux variables. Il permet d’identifier s’il existe une corrélation entre ces variables, c’est-à-dire si elles évoluent de manière similaire ou inversement.
Le diagramme de corrélation permet d’illustrer la relation entre deux phénomènes variables et observer l’influence de l’une sur l’autre. Les deux phénomènes doivent être de nature quantifiable.
Le calcul et le tracé de la droite de régression est très utile pour prévoir la valeur de Y en fonction de X. En effet, il permet d’exprimer sous forme mathématique la relation entre les variables X et Y.
Comment utiliser le diagramme de dispersion ?
Le diagramme de corrélation se présente sous forme d’un graphique où les deux axes, x et y, correspondent à une variable (une mesure d’un phénomène) différente. Par un certain nombre d’expérimentations ou d’observations, où une des deux variables est modifiée, on inscrit un point correspondant aux valeurs des deux variables sur le graphique. On obtient alors un nuage de points, d’où il est possible d’analyser la forme des points et de prédire le comportement de l’une des deux variables (x) en fonction de la variation de l’autre (y).
La relation entre les deux variable est exprimé sous forme d’une équation mathématique : y=f(x). Pour quantifier la relation, il est important de calculer le coefficient de corrélation. Les coefficients de corrélation couramment utilisés incluent le coefficient de corrélation de Pearson, le coefficient de corrélation de Spearman et le coefficient de détermination (r2).
L’utilisation du diagramme de dispersion passe par plusieurs phases :
- Déterminer les deux phénomènes à étudier (Cause-Effet).
- Recueillir les paires de données à utiliser. Pour recueillir ces données on peut se servir d’une fiche de collecte des données adaptée à la situation.
- Tracer la cause sur l’axe des X et l’effet sur l’axe des Y.
- Pointer, sur le graphique, les paires de données.
- Trouver l’équation mathématique qui exprime la relation entre les deux variables. Par exemple dans la cas d’une régression linéaire, la droite de régression a l’équation suivante : Y = aX + b.
- Calculez le coefficient de corrélation pour quantifier la relation entre les deux variables. La relation entre les deux variables est considérée d’autant plus fort lorsque la valeur absolue du coefficient de corrélation s’approche de 1.
- Tracer sur le graphique la fonction f(x).
- Analyser le graphique.
Exemple de diagramme de corrélation
L’exemple suivant illustre la relation entre la taille des enfants et celle des parents.
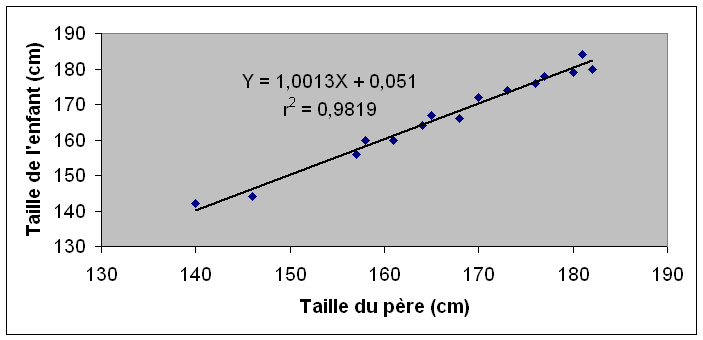
L’analyse du graphique montre que la taille de l’enfant est fortement liée à la taille de son père. Le coefficient de détermination (r2) dans ce cas est très proche de 1.
Conclusion
Le diagramme de corrélation est un outil précieux pour analyser les relations entre les variables. Il offre une compréhension visuelle des données et peut aider à prendre des décisions éclairées en matière de qualité et de gestion.